基石04 - 分布、概率分布

讲完基本概念，下面正常的节奏应该是学统计图表和描述统计。

不，我们不要在各种描述统计的平均数中数众数中，消耗了刚培养起来的学习热情，要把“刚学完绪论后觉得自己非常能学好统计”的学习劲头留给比较难的东西，所以，我们快马加鞭地进入到推论统计。

别担心，我们能跳过描述统计，快速进入推论统计的一大信心是：因为这两者背后的逻辑差的还挺大的，所以你根本不需要知道描述统计的知识就可以学推论统计了。

本章内容：

• 分布是什么意思？

• 概率分布是什么？

• 有哪些需要关注的概率分布？

分布

如果对分布这个词没有实感，我们可以先从中文理解它：一定地区或区域内散布。这个定义里有两个点：第一，散布的主语；第二，散布在哪里。比如：人分布在公园里，矿产分布在岩石里，鱼类分布在海域里。

在统计情境里，主语自然就是数据了。数据分布的位置即数轴，包括数据处于数轴的绝对位置和数据间的相对位置。

对数据来说，数轴是不可见的，但通过作图，分布就能直观地展示了。这也是分布一般用图来表示的原因：在大脑中的数轴可不利于进一步思考噢。

上述关于分布的解释有点不同寻常，但是只要你能理解到就足够。只要你不是真的在试卷上回答「解释分布在统计学中的概念」这道题时，写出我在上面解释的这一通，这样理解分布是没什么问题的。

概率分布

┃概率分布的概念

我们在统计中提到的数据分布，往往指的是数据的概率分布——某个随机变量的某个取值出现的可能性。

概率分布进一步限定了数据分布的主语，主语不是某个数据本身，而是某个数据出现的可能性。

这个概念有些不太接地气，可能需要多花点时间来理解。比如对身高这个随机变量来说，概率分布描述了某个身高在人群中出现的概率，或可能性，而不是某个身高的具体数值。

而对于身高的具体数值分布如何，我们也关心，但是是通过描述统计来完成的。

也是从这个层面上，你可以将描述统计和推论统计区分开来：描述统计是针对样本的具体数据来完成的，是真实的计算；而推论统计是依赖概率和可能性的，是不一定准确的推论。之后所有推论统计的原理，归根结底都是概率。

┃概率分布的分类

和数据一样，概率分布也有很多不同的类型，不同的分布描述了不同概率事件的结果。目前，数学和统计上最常用的概率分布有十几种，感兴趣可以大概瞅一眼。

它们各自不同，但也可以相互转化，正态分布是它们其中的绝对C位，其他的概率分布都可以用数学转换的方式转化成正态分布，可以去这个视频围观一下。

最大类的区分是连续分布和离散分布，分别针对连续变量和离散变量的分布。

在心理统计中，最常用的连续随机变量分布是正态分布，最常见的离散变量分布是二项分布。

另一个重要的区分是基本随机变量的分布和基本随机变量函数的分布，后者也叫抽样分布，之后我们都会用抽样分布这个词。

具体来说，基本随机变量的分布描述了某个随机变量的取值的概率情况，比如身高。

抽样分布则描述了对一组身高样本进行进一步计算所得的统计量的分布，如均值、方差、标准差等的分布，这一组身高样本是从身高总体中抽取的。

抽样分布关注的不是总体的分布，也不是具体样本的分布，而是从总体中抽取的所有样本的均值、方差、标准差等的概率分布如何。

知道了这个，我们就掌握了从总体中可以抽取到的所有样本的均值等统计量的分布规律，那么我们手里这个单一确定的样本，它的均值等统计量就可以被还原到抽样分布中的一个具体的位置，借由这个位置，我们可以进一步推论总体性质。

抽样分布是抽样调查能够进行的最重要数理依据，正是有了抽样分布的规律，我们才真的可以做抽样调查，用样本来推论总体。也就是上一节中我们提到的：统计学保障。

可以说理解透了抽样分布，推论统计就全通了。我们在05中详细讲。

┃课本的分类和分类标准

下图是课本上对概率分布的分类标准和类型：

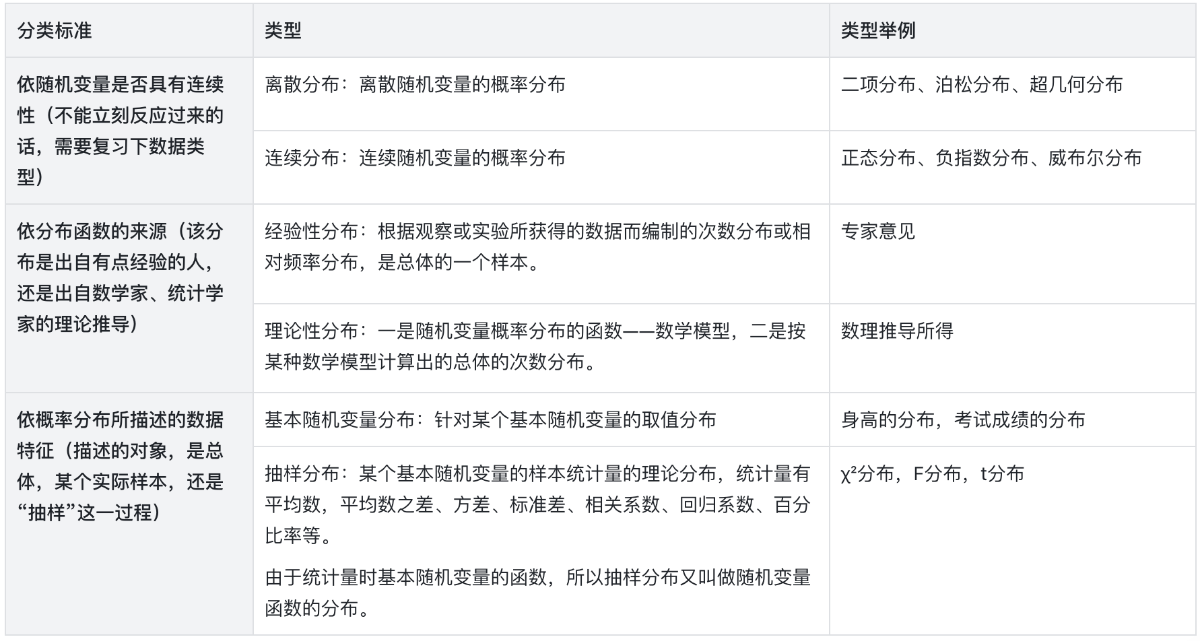
对于这些分布，我们需要知道的是：

1、基础统计的学习阶段，最常接触到的概率分布有以下几种：正态分布、二项分布、t分布、F分布和χ²分布等，后三个属于抽样分布；其他的概率类型可能会在高级统计中用到，暂时可以先保持一无所知。

2、除非题目特别提到，大部分情况下我们都用的是理论分布，经验分布一般只出现在例如专家意见、校长意见这样的描述下，相当于从总体中抽了一个样本，用这个样本的统计量直接替代总体参数。

3、抽样分布和总体分布的区分，是非常重要的考点，也是推论统计重要的理解点，之后的大部分计算题其实都是在考察抽样分布。我们会在05单独讲抽样分布，到时候要打起精神来！

接下来，我们会按照顺序，逐一分析每个分布的特点。