6. 费米估算

费米估算，是一个很小众，但是可以在日常中经常使用的一个思维工具。

比如，应届生面试的时候，会被问到这样的面试题：

• 估算杭州每年奶茶店的规模大小？
• 估算广州市有多少个理发店？
• 估算成都双流机场的人流量有多大？

……

工作的时候，要做一个产品的市场规模测算，比如，测算一个城市有多少家奶茶店，你们进入这个市场有多大概率赚到钱。

只要搞明白费米估算，就可以很好解答地这些问题，在日常工作中也能把复杂的问题简单化，进而更容易解决问题。下面我们好好学习一下什么是费米估算。

什么是费米估算？

费米是美国著名的物理学家，在1938年获得过诺贝尔物理学奖，费米估算是他提出的。

费米估算法的原理是，在求解一个看似不能解决的数量问题时，将总问题分解成几个次级问题甚至是再次级问题，直到每个次级问题不用，求教专家或书本都能解答(即转化为一些常识问题时)，总问题即可迎刃而解。

费米估算思想的核心：逻辑拆解。

也就是说把一个庞大的、抽象的、复杂的问题，逐级拆解为微小的、具体的、简单的问题，然后再将这些小问题进一步拆解，只要保证了逻辑关系，那么将这些可以回答的小问题答案，逐步反推到费米问题上，就可以得到最终的准确答案。

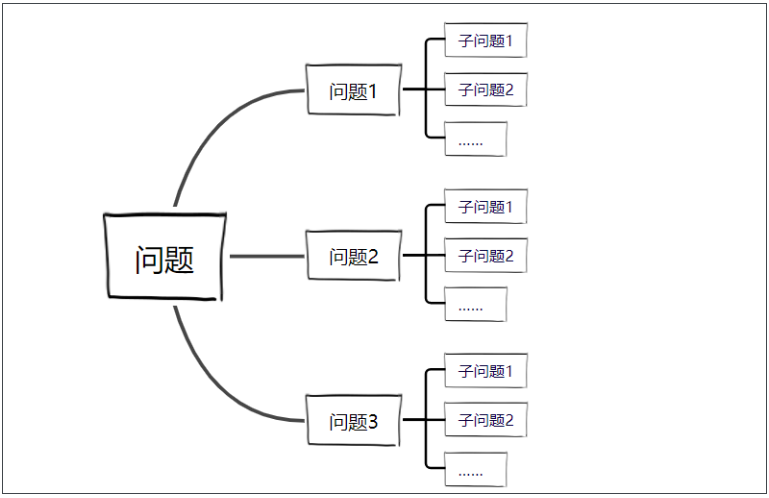
下面来看看这个思维工具是怎么运用的。

1938年，他在芝加哥大学课堂上，提出的一个问题，这个问题造就了著名的“费米估算”。

他问学生：“芝加哥有多少个钢琴调琴师？”

听到这个问题，学生们一脸懵逼。

第一步：拆解

费米则告诉学生：将复杂的问题拆解成小的、可知结果的部分。

要解决这个问题，首先第一步要按逻辑拆解问题。

回到费米提出的问题，我应该如何进行拆解呢？

费米将钢琴师的人数问题，拆解成每年芝加哥全部调音师工作的时长，以及一位调音师每年的工作时间。

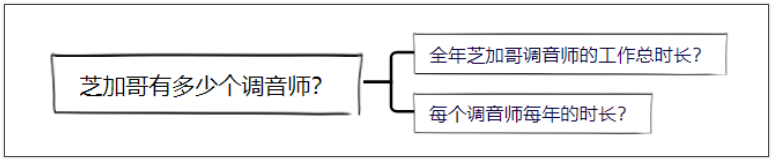而这样拆解的逻辑是：总人数=总时长/每人时长

那芝加哥全部调音师的总工作时长该如何计算呢？可以继续对总工作时长进行拆解：

• 芝加哥的总钢琴的数量。
• 每架钢琴多久需要调一次音量？
• 一位调音师调音的时长。

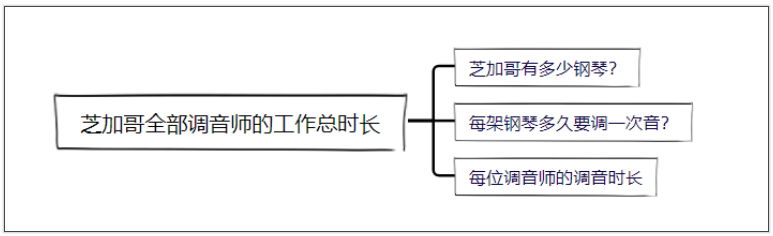拆解的逻辑就是：

所有调音师的工作总时长=钢琴数每年调音次数调音时长

这个问题拆解到这里就差不多可以估算出来了，继续拆解下去的意义也不大。

那么问题来了，现在的三个问题如何进行估算呢？其实费米也告诉了我们方法。

第二步：估算的合理赋值

对于基本问题的估算，费米给出了一个天才式的估算方法：对于小问题的估算，不要估算其本身而是估算其上下界然后在10倍的范围内估算出数值。

也有很多朋友说，我们可以按照数据或者经验来赋予较为准确的范围。

这倒也没有错，但切记要考虑赋值的上界和下界。

按照这个赋值方法，我们看下费米是如何估算的。

首先费米知道了芝加哥的总人口（官方数据）为300万人，平均每个家庭约4人，那么芝加哥就有75万个家庭。

这些家庭中有多少架钢琴呢？

在当时的美国，钢琴是半奢侈品，费米估算拥有钢琴的家庭不会超过1/2，也不会低于1/10。

因此费米估算为1/3，那么芝加哥就有75*1/3=25万架钢琴。

再看第二个问题，每架钢琴每年要调几次音？

费米估算，应该不会超过一年3次，也不会低于10年1次，他觉得3年调一次音是合理的。因此，每年架钢琴一年要调0.33次音。

最后一个问题，每架钢琴调音一次要多久？

不会超过10小时，也不会低于1小时，因此费米估算是3小时。

那么第一个大问题就解决了。

芝加哥全部钢琴的总调音时长是：

2500000.333=249000

继续估算下一个问题——芝加哥每个调音师的工作时长。

一年有52个星期，一个调音师一周工作5天，算上假期和加班时间，估计一个调音师一年的工作日是250天，还要扣除花在在路上的时间，则每天的实际工作时间是240.6=14.4小时。那么他一年的工作时间是25014.4=3600小时。

249000/3600=69

最终的结果可以算出来了，芝加哥大约共有69名调音师。

那么实际上有多少人呢？

事后有人通过电话簿进行统计，芝加哥大概有80名调音师，除去号码相同的，结果竟然相差无几。

那可能有人会问，如果费米估算中家庭拥有钢琴的家庭改为1/4，而不是1/3，结果不就会变了呢？费米的每次估算都会那么准确吗？

这就涉及到估算的平均律问题了！

估算平均律

估算过程总不可避免地存在误差，每个步骤中的估算误差会对结果造成显著影响吗?就单个估算误差来讲，可能会对结果造成显著影响，甚至是与实际值相差很大。但当多个步骤中都存在估算误差时，这些估算误差非常可能会相互抵消，最终对估算结果造成的影响并不非常显著。这就是平均律。

意思是说，在任何一组的计算中，估算带来的错误都可以互相抵消，假设越多，被抵消的概率就越大。

如图，估算假设有的高，有的低，但如果这些“点”的数量足够，最终误差就会被相互抵消，整体估算误差最终会趋于平均值。

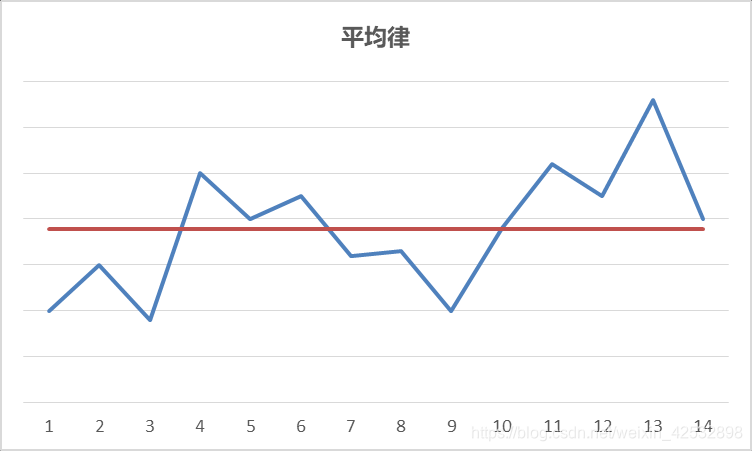在费米估算过程中，不是只有一次估算，而是有一系列的估算。

比如估算芝加哥有1/3家庭有钢琴，同时也会估算一架钢琴平均5年调一次音。

这些估算有的过高有的过低，相乘之后会相互抵消，回归到较为准确的平均值。

而且，有个很重要的前提，我们的估算值是有实际数据或者生活经验支撑的。

估算值不能偏离实际结果太远，要从实际结果、常识出发。

比如费米在估算芝加哥每个家庭有4个人，换成我们来估算的话，我们不能拍脑袋直接估算芝加哥每个家庭有10个人。

我是总结

到这里，费米估算也介绍得差不多了。照例总结一下，费米估算就4个步骤：

1. 明确问题
2. 分析是需求端问题还是供给端问题，或者两个角度都不是
3. 问题拆解，列公式
4. 计算

对问题进行拆解时，我们提倡按照相互独立、完全穷尽（MECE，Mutually Exclusive Collectively Exhausted）的原则 ，将问题层层拆解成子问题，从而找到问题的根源。

在进行费米估算时，要注意两个点：

①避免把未知数拆解成新的未知数（而应该要让拆解后的元素变得可解决）

②估算要有实际数据和生活经验作为支撑。

总而言之，费米估算是在极其有限的条件下，通过拆解未知并利用身边的信息来求解出结果的方法。

而这个方法也告诉我们，遇到一个复杂未知的问题时，可以通过拆解问题，层层解剖，最终逐步逼近结果。

面对不确定性，我们不应停滞不前，而是要懂得抓住身边有价值信息，快速决策。